اشاره: توضیح نظم از خلال کثرتی که شخصیت چیزها و مرز آن‌ها با چیزهای دیگر را تدارک می‌بیند، کاری است که با پیدا کردن خصوصیات مشترک و ذاتی چیزها دنبال می‌شود و آن‌ها را ذیل یک تعریف، می‌پیراید. اما توضیح چرایی بیرون‌زدگی چیزها از این نظم تعریفی، اگر نتواند توضیحی موجه باشد، عمل تعریف را به کلی بیهوده می‌سازد. چرا که در این صورت، تعریف هیچ واقعیتی از چیزها به ما نمی‌گوید. ریچارد ددکیند ریاضیدان مشهور آلمانی، یکی از دانشمندانی بود که مسئله رابطه نظم و فردیت چیزها را از خلال مسئله ریاضیاتی پیوستگی دنبال کرد. به همین دلیل و علی‌رغم تلاشی که خود او برای ارائۀ اثباتی ساده و عمومی برای پیوستگی داشت، پذیرش شهودی پیوستگی که از ناحیه درک هندسی، میسر بود، برای وی کفایت نمی‌کرد. او می‌خواست واقعا بداند که اعداد چگونه در عین حالی که از یکدیگر متمایزند، پیوستاری قابل اشاره می‌سازند.

*عکس تصویر یک لوح هندی (228-343 پس از میلاد) از نسخه خطی بخشعلی که استفاده از نقطه را به عنوان صفر آخرین خط نشان می‌دهد. کتابخانه‌های بودلیان، دانشگاه آکسفورد

پیشگفتار ویراست اول

در علم هر چیز که قابل اثبات است نباید بدون اثبات پذیرفته شود. گرچه این درخواست بسیار معقول به نظر می‌رسد، اما به گمان من در بنیادگزاری ساده‌ترین علم، یعنی آن بخش از منطق که با نظریة اعداد سروکار دارد، حتی در جدیدترین توصیفات آن، نیز به هیچ وجه بدان توجه نمی‌شود. در ضمنِ اینکه من حساب (جبر و آنالیز) را فقط یک بخش از منطق لحاظ می‌کنم، اعلام می‌کنم که مفهوم عدد را کاملاً مستقل از تصورات یا شهودهای مکان و زمان در نظر می‌گیرم، و مفهوم عدد را پیامد بی‌واسطۀ قوانین محض اندیشه می‌دانم. بنابراین پاسخ اصلیِ من به پرسشی که در عنوان این نوشته طرح شده به‌طور خلاصه از این قرار است: اعداد مخلوقات آزاد روح آدمی‌اند، و به‌عنوان ابزاری برای درک آسان‌تر و سریع‌تر تفاوت بین چیزها عمل می‌کنند. تنها از طریق برساخت کاملاً منطقی علم اعداد و با حصول قلمرو اعداد پیوسته در آن [علم اعداد] است که ما به درستی در وضعیتی قرار می‌گیریم که به‌دقت دربارۀ تصوراتمان از مکان و زمان پژوهش کنیم، تا نسبتی بین مکان و زمان و این قلمرو اعداد، که در روح‌مان خلق کرده‌ایم، برقرار سازیم. اگر به‌دقت آنچه را که در شمارش مقدار یا تعداد چیزها انجام می‌دهیم بررسی کنیم، می‌توانیم این توانایی روح را ببینیم که چیزها را به چیزها مرتبط می‌سازد و اجازه می‌دهد که یک چیز با چیز دیگر متناظر شود، یا یک چیز به‌واسطۀ چیز [دیگر] به نمایش درآید، و بدون این توانایی، اندیشیدن ممکن نیست. همانطور که من قبلاً در اعلام این نوشته بیان کرده‌ام، به نظر من، کل علم اعداد باید بر روی این بنیاد منحصربه‌فرد و ضروری برپا شود. من نیت چنین توصیفی را پیش از انتشار نوشته‌ام در باب پیوستگی پرورانده بودم، اما تازه پس از انتشار آن و با وقفه‌های بسیاری که به علت وظایف رسمی و کارهای ضروری دیگر پیش آمد، در سال‌های 1872 تا 1878 توانستم نخستین پیش‌نویس را روی کاغذ بیاورم، طرحی که چندین ریاضیدان آن را بررسی و تا حدودی دربارۀ آن با من بحث کردند. [آن طرح] همین عنوان را داشت و، اگرچه نه در بهترین ترتیب، شامل تمامی ایده‌های اساسی نوشتۀ کنونی من، که فقط تکمیل محتاطانۀ آن است، بود؛ به‌عنوان نکات اصلی، من در اینجا به این موارد اشاره می‌کنم: تمایز حاد متناهی از نامتناهی، مفهوم تعداد [Anzahl] چیزها، اثبات اینکه نحوۀ استدلالی که با عنوان استقرای تام (یا استنتاج n+1 از n) می‌شناسیم واقعاً مدلل و قاطع است، و اینکه بنابراین تعریف با استقرا (یا بازگشت) قطعی و بدون تناقض است.

هر کس از آنچه معمولاً عقل سلیم نامیده می‌شود برخوردار باشد می‌تواند این نوشته را بفهمد؛ ابداً نیازی به شناخت ِ فنی ِ فلسفی یا ریاضیاتی نیست. اما من احساس می‌کنم که خواننده در اشکال مبهمی که من پیش رویش می‌گذارم به‌سختی اعداد خویش را که در تمام طول زندگی‌اش همچون دوستانی باوفا و نزدیک همراهیش کرده‌اند تشخیص خواهد داد؛ او از زنجیرۀ بلند استنتاج‌های سادۀ متناظر با فهم گام‌به‌‌گام ما خواهد ترسید، از کالبدشکافی خشک و سرد زنجیره‌های اندیشه که قوانین اعداد مبتنی بر آن هستند خواهد ترسید، و از اینکه مجبور است اثبات حقایقی را دنبال کند که برای شهود درونی مفروضش از همان اول روشن و قطعی به نظر می‌رسند ناشکیبا خواهد شد. برعکس، من دقیقاً در امکان بازگرداندن و تحلیل چنین حقایقی به حقایق ساده‌تر، خواه زنجیرۀ استنتاج بسیار طولانی یا ظاهراً مصنوعی باشند خواه نه، برهانی متقاعدکننده را تشخیص می‌دهم که داشتن آن‌ها یا باور به آن‌ها هرگز به‌صورت بی‌واسطه از طریق شهود درونی به دست نمی‌آید، بلکه همواره تنها با تکرار کم و بیش کامل استنتاج‌های منفرد حاصل می‌شود. من می‌خواهم این عمل اندیشه را که پی‌گیری آن به دلیل سرعت بالایش بسیار دشوار است با عملی مقایسه کنم که یک خوانندۀ کاملاً ماهر در خواندن انجام می‌دهد؛ چنین خواندنی همواره تکرارِ کم و بیش کاملِ گام‌های منفردی باقی می‌ماند که فرد مبتدی در هجی‌کردنِ پرزحمت خود برداشته است؛ اما مقدار بسیار کوچکی از همان، و بنابراین تلاش و کوشش بسیار کم روح، برای خوانندۀ حرفه‌ای کافی است تا کلمۀ صحیح و درست را، البته فقط با احتمال بسیار زیاد، تشخیص دهد؛ چون همانطور که معروف است، هر از گاهی حتی از زیر دست ماهرترین نمونه‌خوان‌ها هم خطایی چاپی در می‌رود، یعنی، چیزی را غلط می‌خوانند که اگر زنجیرۀ افکار مرتبط با هجی‌کردن به‌طور کامل تکرار شده بود، [چنین خطایی] غیر ممکن می‌بود. بنابراین، از زمان تولد، به‌طور مداوم و به‌نحوی فزاینده ما به سوی مرتبط ساختن چیزها با چیزها و بدین ترتیب استفاده از آن قابلیت روح رهنمون می‌شویم که خلق اعداد مبتنی بر آن است؛ از طریق تکرار این تجربه که به‌نحوی لاینقطع، اگرچه بدون هدفی مشخص، در اولین سال‌های زندگی ما رخ می‌دهد و تشکیل حکم‌ها و زنجیره‌های استدلال همراه با آن، ما به اندوخته‌ای از حقایق حسابی اصیل دست می‌یابیم که بعدها نخستین معلمان ما به آن‌ها به‌مثابۀ چیزی ساده، بدیهی و داده شده در شهود درونی اشاره می‌کنند، و بنابراین چنین رخ می‌دهد که بسیاری از مفاهیم بسیار پیچیده و اصیل (برای مثال تعداد چیزها) اشتباهاً ساده تلقی می‌شوند. در این معنا، که آن را با کلماتی بیان می‌کنم که از روی یک ضرب‌المثل معروف، 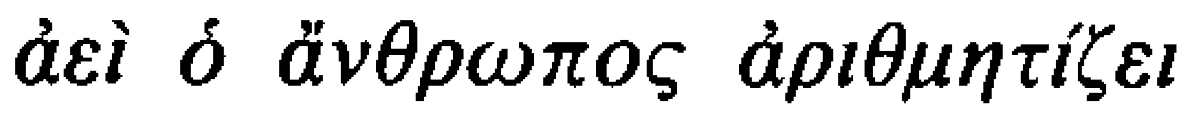 (انسان همواره حساب می‌کند) ساخته شده است، امیدوارم صفحاتی که در ادامه می‌آیند، به‌عنوان تلاشی برای استقرار علم اعداد بر بنیادی یکپارچه، پذیرش مساعدی بیابند و دیگر ریاضیدانان ترغیب شوند تا زنجیره‌های بلند استنتاج را به مقیاسی بی‌پیرایه‌تر و مطبوع‌تر برگردانند. 

بر حسب هدف این نوشته، من خود را به ملاحظۀ سلسلۀ به‌اصطلاح اعداد طبیعی محدود می‌کنم. اینکه بعداً به چه طریق بسط تدریجی مفهوم عدد، خلق صفر، اعداد منفی، اعداد کسری، اعداد اصم و اعداد مختلط به‌طور پیوسته با تقلیل به مفاهیم اولیه‌تر و بدون مداخلۀ هیچ تصور خارجی (مثل مفهوم مقادیر اندازه‌پذیر)، که طبق فهم من می‌توانند تنها از طریق علم اعداد وضوح کامل بیابند، انجام شده است، من این را حداقل برای مثالِ اعداد اصم در نوشتۀ قبلی خودم در باب پیوستگی (۱۸۷۲) نشان داده‌ام؛ همانطور که قبلاً اشاره کرده‌ام، می‌توان به طریقی کاملاً مشابه، به توسعه‌های دیگر پرداخت، و من این را برای خود محفوظ می‌دارم که [روزی] نمایشی منسجم از این موضوع ارائه دهم. دقیقاً از این منظر، همچون چیزی بدیهی و نه کاملاً جدید، آشکار می‌شود که هر قضیۀ جبر و آنالیز مرتبۀ بالاتر، هر چقدر هم که دور باشد، را می‌توان به‌عنوان قضیه‌ای دربارۀ اعداد طبیعی بیان کرد، ادعایی که من بارها از زبان دیریشله^[1] شنیده‌ام. اما برخلاف دیریشله، من ابداً چیز تحسین‌برانگیزی در این اطناب پرزحمت و پافشاری بر استفاده از اعداد طبیعی و به رسمیت نشناختن هر چیزی دیگری به غیر از آن نمی‌بینم. بر عکس، بزرگترین و مفیدترین پیشرفت‌ها در ریاضیات و علوم دیگر همواره با خلق و معرفی مفاهیم جدید صورت گرفته‌اند، پس از آنکه [ابداع این مفاهیم جدید] با تکرار مکرر پدیده‌های مرکبی که تنها با دشواری زیر سلطۀ مفاهیم قدیمی می‌روند، ضرورت یافته است. من در تابستان ۱۸۵۴ به مناسبت پذیرشم به‌عنوان دانشیار غیررسمی در گوتینگن^[2] در دانشکدۀ فلسفه در باب این موضوع یک سخنرانی ایراد کرده‌ام که گاوس^[3] نیز نیت آن سخنرانی را تایید کرد؛ اما اینجا مجال پرداختن به جزئیات بیشتر دربارۀ آن وجود ندارد.

در عوض از فرصت استفاده می‌کنم تا نکاتی مربوط به کار قبلی‌ام، که در بالا به آن اشاره شد، در باب پیوستگی و اعداد اصم مطرح کنم. نظریۀ اعداد اصم که در آنجا ارائه شده است و من آن را در پاییز 1853 به پایان رساندم، مبتنی بر پدیداری است که در قلمرو اعداد گویا رخ می‌دهد (بخش 4)، و من آن را برش می‌نامم و من نخستین کسی بودم که به‌طور دقیق درباره‌اش پژوهش کردم، و این پژوهش به اثبات پیوستگی قلمرو جدید اعداد حقیقی منتهی شد. به نظر من این نظریه از دو نظریه‌ای که متفاوت با این نظریه و همچنین متفاوت با یکدیگر هستند و آقایان وایرشتراوس^[4] و جی. کانتور^[5] آن‌ها را مطرح کرده‌اند و دقت کاملی نیز دارند،  نسبتاً ساده‌تر است، می‌خواهم بگویم بی سر و صداتر است. این نظریه بعدها بدون تغییر اساسی از سوی آقای او. دینی^[6] در die Fondamenti per la teorica delle funzioni di variabili (Pisa 1878) مورد استقبال قرار گرفت؛ اما این واقعیت که در خلال این ارائه به نام من، نه در توصیف پدیدۀ کاملاً ریاضیاتیِ برش، بلکه تصادفاً در جایی اشاره می‌شود که نویسنده دربارۀ وجود یک مقدار اندازه‌‌پذیرِ متناظر با برش بحث می‌کند، ممکن است به آسانی منجر به این فرض شود که نظریۀ من مبتنی بر در نظر گرفتن چنین مقادیری است. هیچ چیز نمی‌تواند نادرست‌تر [از این] باشد؛ بلکه من در بخش 3 مقاله‌ام دلایل مختلفی اقامه کرده‌ام که چرا به کلی دخالت مقادیر اندازه‌پذیر را رد می‌کنم، و به‌ویژه من در پایان مقاله دربارۀ وجود آن‌ها اشاره کرده‌ام که برای بخش بزرگی از علم مکان، پیوستگی برساخت‌های آن حتی یک شرط ضروری هم نیست، گذشته از این واقعیت که اگرچه در کارهای مربوط به هندسه، نام حساب تنها به‌نحو اتفاقی ذکر شده اما هرگز به‌طور واضح روشن نشده است و بنابراین نمی‌تواند برای اثبات به کار گرفته شود. برای توضیح بیشتر این موضوع به مثال زیر اشاره می‌کنم. اگر ما سه نقطۀ غیر همراستای A, B, C را به دلخواه انتخاب کنیم، تنها با این محدودیت که نسبت فواصل AB, AC, BC اعداد جبری باشند و تنها آن نقطه‌ای M را موجود در مکان در نظر بگیریم که نسبت‌های AM, BM, CM به AB هم اعداد جبری باشند، آنگاه مکانی که با این نقطۀ M به وجود می‌آید، همانطور که دیدنش آسان است، در همه جا ناپیوسته است؛ اما علیرغم این ناپیوستگی، و با وجود شکافها در این مکان، تمامی برساخت‌هایی که در کتاب اصول اقلیدس ظاهر می‌شوند، تا جایی که من می‌توانم ببینم، درست مانند مکاںݐݭݭِ کاملاً پیوسته، دقیقاً قابل تحقق هستند؛ به ناپیوستگی این مکان در علم اقلیدسی اصلاً توجه نمی‌شود، اصلاً حس نمی‌شود. اما اگر کسی بگوید ما نمی‌توانیم به مکان مگر به‌صورت پیوسته بیندیشیم، من به خود جرأت شک کردن در آن را می‌دهم و توجه را به این واقعیت جلب می‌کنم که برای فهم واضح ماهیت پیوستگی و دریافتن اینکه در کنار روابط کمّی گویا، روابط اصم و در کنار روابط کمی جبری، روابط کمی متعالی نیز قابل فهمند به یک آموزش علمی پیراسته و بسیار پیشرفته نیازمندیم. از همه زیباتر به نظرم می‌رسد که بدون هیچ تصوری از مقادیر اندازه‌پذیر و تنها با یک سیستم متناهی گامهای فکر ساده، انسان می‌تواند در خلق قلمرو اعداد پیوسته و محض به پیش رود؛ و به نظر من تنها بدین وسیله برای او ممکن است که مفهوم مکان پیوسته را واضح و روشن ارائه دهد.

همان نظریۀ اعداد گنگ مبتنی بر پدیدۀ برش در مقدمه à la théorie des fonctions d’une variable نوشتة جی. تانری^[7]  (Paris,1886) ارائه شده است. اگر من فقره‌ای در پیشگفتار این کتاب را به‌درستی فهمیده باشم، نویسنده این نظریه را مستقلاً طرح کرده است، یعنی، در زمانی که نه‌تنها نوشتۀ من، بلکه Fondamenti دینی نیز که در همین پیشگفتار به آن اشاره شد، برای او ناشناخته بوده است؛ این هماهنگی در نظر من برهانی مسرت‌بخش است که دریافت من با ماهیت امر متناظر است، واقعیتی که ریاضیدانان دیگری هم مثل آقای ام. پاش^[8] در مقدمه‌ای بر حساب دیفرانسیل و انتگرال خود  (Leipzig, 1883) آن را به رسمیت شناخته است. اما من نمی‌توانم با خیال آسوده با آقای تانری موافق باشم که این نظریه را توسعۀ یکی از اندیشه‌های جی. برتراند^[9] می‌خواند که در Traité d’arithmétique متعلق به او ظاهر می‌شود و در آنجا وجود دارد، و برحسب این اندیشه یک عدد اصم با ذکر تمامی اعداد گویای کوچکتر و بزرگتر از آن به‌مثابۀ اعداد معرف تعریف می‌شود. دربارۀ این جمله که توسط آقای او. استولز^[10] -ظاهراً بدون تحقیق دقیق- در پیشگفتار بخش دوم کتاب وی درسگفتارهایی دربارۀ حساب عمومی (Leipzig, 1886) تکرار شده است، اجازه می‌خواهم که ملاحظات زیر را ذکر کنم. این عقیده که یک عدد اصم در واقع با دستوری که هم‌اکنون توصیف شد به‌عنوان عددی کاملاً تعریف‌شده در نظر گرفته شده است، بی‌تردید مدت‌ها پیش از آقای برتراند نزد تمامی ریاضیدانانی که روی مفهوم اصم کار می‌کردند متداول بوده است؛ هر محاسبه‌گری که ریشۀ اصم یک معادله را با تخمین محاسبه می‌کند دقیقاً همین شیوۀ تعیین کردن را در پیش چشم خود دارد؛ و اگر، همانطور که آقای برتراند منحصراً در کتابش (ویراست هشتم، سال 1885، پیشِ روی من است) انجام داده است، اعداد اصم را به‌مثابۀ نسبت مقادیر اندازه‌پذیر در نظر بگیریم، پس این شیوۀ تعیین آن‌ها پیش از این در روشن‌ترین طریق ممکن در تعریف مشهوری که اقلیدس از تساوی دو نسبت به دست داده است ارائه شده است.(Elements, V, 5)  یقیناً همین عقیدۀ باستانی خاستگاه نظریۀ من و نیز نظریۀ آقای برتراند و بسیاری تلاش‌های کمابیش صورت‌گرفته بوده است تا ورود اعداد اصم به علم حساب را موجه نماید. اما اگر به‌طور کامل و به‌کلی با آقای تانری موافقت کنیم، اما در یک بررسی واقعی باید بلافاصله اشاره کنیم که طرح آقای برتراند، که در آن به پدیدۀ برش در خلوص منطقی‌اش حتی یک بار هم اشاره نشده است، مطلقاً هیچ شباهتی به طرح من ندارد، چون او بلادرنگ به وجود یک مقدار اندازه‌پذیر متوسل می‌شود، مفهومی که من به دلایلی که در بالا اشاره کردم آن را کاملاً رد می‌کنم؛ و صرف‌نظر از این واقعیت، به نظرم این توصیف در تعاریف و براهین بعدی، که  بر فرض وجود این مقدار اندازه‌پذیر مبتنی هستند، نیز دیده می‌شود و بدین ترتیب شکاف‌هایی بسیار اساسی را عرضه می‌کنند که من در نوشته‌ام (۶§) ذکر کرده‌ام یعنی این ادعا که قضیۀ √2∙ √3=√6 در هیچ جا هنوز به‌طور اکید اثبات نشده است، که با توجه به این اثر و نیز با در نظر گرفتن بسیاری از آثار دیگر که در آن زمان با آن‌ها آشنا نبودم موجه است.

هارتزبورگ، ۵ اکتبر ۱۸۸۷
ر. ددکیند 

پیشگفتار ویراست دوم

نوشتۀ پیش رو بلافاصله پس از انتشارش با قضاوت‌های مساعد و نیز نامساعدی مواجه شد، و در واقع اشتباهات و خطاهای جدی آن سرزنش شد. من نتوانستم خود را نسبت به درستی و حقانیت این اتهامات متقاعد کنم و اکنون ویراست جدیدی از آن یادداشت را که برای مدتی نایاب بود بدون هیچ تغییراتی منتشر می‌کنم و تنها چند نکتۀ زیر را به پیشگفتار نخست می‌افزایم.

جی. کانتور (Ein Beitrag zur Mannigfaltigkeitslehre, Crelle's Journal, Vol. 84, 1878) و همچنین بولتزانو  (Paradoxien des Unendlichen, § 20, 1851) پیش از انتشار نوشتۀ من به آن ویژگی که من به‌عنوان تعریف سیستم نامتناهی از آن استفاده نموده‌ام اشاره کرده بودند. اما هیچ کدام از این نویسندگان نکوشیدند از این ویژگی برای تعریف امر نامتناهی استفاده کنند و بر این اساس علم اعداد را با منطقی دقیق تأسیس کنند، و محتوای کار پرزحمت من دقیقاً همین بود، کاری که به تمامی اساساً چندین سال پیش از انتشار رسالۀ کانتور تمام شده بود و در زمانی که حتی نام کار بوالتزانو^[11] را نشنیده بودم. به خاطر کسانی که به چنین پژوهشی علاقه‌مندند و دشواری‌های آن را می‌فهمند، نکاتی را که در ادامه می‌آید اضافه می‌کنم. ما می‌توانیم تعریفی کاملاً متفاوت از امر متناهی و نامتناهی وضع کنیم، که تاحدی ساده‌تر به نظر می‌رسد زیرا مفهوم شباهتِ یک تصویر حتی فرض نشده است، به عبارت دیگر:

«گفته می‌شود سیستم S متناهی است اگر بتوان آن را به‌نحوی در خودش تصویر کرد که هیچ بخش حقیقی از S به خودش تصویر نشود؛ در غیر این صورت گفته می‌شود که S یک سیستم نامتناهی است».

حال بیایید تلاش کنیم تا عمارت خودمان را بر روی این بنیاد جدید بنا کنیم! ما به‌زودی با مشکلات بزرگی مواجه خواهیم شد، و من مجازم ادعا کنم که اثبات موافقت کامل این تعریف با [تعاریف] قبلی تنها (و بنابراین به‌راحتی) زمانی می‌تواند حاصل شود که ما اجازه داشته باشیم دنبالۀ اعداد طبیعی را از پیش بسط‌یافته فرض کنیم و از ملاحظات نهایی در (131) کمک بگیریم؛ و هنوز چیزی در مورد تمامی این چیزها نه در یک تعریف و نه در تعریف دیگر گفته نشده است! از اینجا می‌توانیم ببینیم که برای چنین تغییر شکلی در یک تعریف تعداد گام‌هایی که در تفکر نیاز است چقدر زیاد است.

حدود یک سال پس از چاپ نوشته‌ام با مبانی حساب فرگه^[12] آشنا شدم، که پیشتر در سال 1884 منتشر شده بود. با اینکه نظر فرگه در آن اثر دربارۀ ماهیت عدد با نظر من فرق داشت، اما، به‌خصوص از ۷۹§ به بعد، حاوی نکاتی بسیار نزدیک به تعریف من بود. مطئمناً کشف این توافق به دلیل تفاوت در شکل بیان آسان نیست؛ اما قاطعیت بیان نویسنده (فرگه) وقتی که از استنتاج منطقی n+1 از n سخن می‌گوید به آسانی نشان می‌دهد که او در این مورد روی همان زمینی ایستاده است که من ایستاده‌ام.

در طی این مدت (۱۸۹۱ تا ۱۸۹۰) درسگفتارهای جبر و منطق شرودر^[13] تقریباً به‌طور کامل منتشر شده است. در این جا ممکن نیست که در خصوص اهمیت این اثر بسیار بکر که برای من بسیار ارزشمند و محترم است، بیشتر صحبت کنم؛ فقط می‌خواهم پوزش بخواهم که علی‌رغم نکاتی که در صفحۀ 253 بخش یک آمده است، من هنوز نمادگذاری‌های نسبتاً ناشیانۀ خود در [8] و [17] را حفظ کرده‌ام؛ هیچ ادعایی برای اتخاذ آن‌ها به‌صورت عام وجود ندارد بلکه تنها قرار است در خدمت هدف این نوشته در باب حساب باشند که به نظر من در اینجا بهتر از نمادهای جمع و ضرب عمل می‌کنند.

هارتزبورگ، ۲۴ آگوست ۱۸۹۳
ر. ددکیند